StealthEscape CS 175: Project in AI
Welcome to Stealth Escape!
Project Summary
The Stealth Escape project aims to develop a reinforcement learning (RL) agent capable of solving a maze within Minecraft via Project Malmo. The goal of the agent is to escape the maze while avoiding dangers such as lava pits and patrolling zombie guards. The agent is trained to make decisions based on its current state (position, light levels, and proximity to obstacles) and adapt its behavior to minimize the risk of falling into hazards or being caught by guards. By leveraging Q-learning and a reward-based system, the agent’s actions are refined over time, improving its ability to achieve the mission’s goal. The continuous learning aspect in RL hones in the pathfinding and decision-making techniques through trial and error as the agent learns to balance exploration with path exploitation to achieve its objective.
The task is challenging on several accounts. Since the environment is dynamic and partially observable-the agent cannot witness the maze as a whole and must respond to the moving guards and hazards in real time-it also has to manage competing objectives: finding the exit, avoiding lava, and remaining undetected by guards. Such environments make traditional rule-based approaches ineffective because they are not adaptable to unpredictable changes or lack the capability of learning from experiences. This is where reinforcement learning becomes significant. RL is when an agent learns through trial and error and improves strategies based on rewards and punishments. For example, it may be that an agent gets a reward for reaching the exit but is punished for falling into lava or being caught by the guard. Hence, the agent learns how to navigate the maze more efficiently over time.
Through this problem, the StealthEscape project can showcase what AI can do for difficult challenging real-life problems with varying uncertainties, dynamic obstacles, and adaptive decision-making. The skills acquired by the agent, such as hazard avoidance or navigation in stealthy ways, have widespread applicability beyond the gaming world-for example, in robotics and autonomous systems. Ultimately, the project would show the efficacy of RL in training agents for functionality in unpredictable and hazardous environments.
Approaches
For our final model, we built it on an earlier Q learning network that trained the agent to move through the maze with zombies and lava (dangers). Previously the agent could only access its position, nearby zombies, and lava locations to choose from a few actions(forward, turn left, and right). Also, we used a fixed reward system, where the agent was awarded 100 points for reaching the goal, and -100 for hitting any dangers. We utilized experience replay and periodic network updates to help improve the Q-values.
One advantage of our baseline approach is that it is simple and efficient, it is easy to implement, and computationally light, so it trains faster and doesn’t require large amounts of data. It is also stable since the Q-values are updated periodically and rewards are fixed. The disadvantages of our baseline approach included limited observational space and action space. Using only basic position tracking meant that the agent couldn’t effectively assess cues in the environment and limited the ability to make nuanced decisions. Using a fixed reward system also doesn’t encourage exploration or safer decision-making beyond simply reaching the goal. The agent relied too much on static environments, so it was hard to generalize.
Initialize Q-values Q(state, action) arbitrarily
Initialize target Q-network and Q-network models
Initialize replay buffer, optimizer
Set epsilon = EPSILON_START
For each cycle:
Initialize state s
total_reward = 0
While mission is running:
Choose action a using epsilon-greedy policy (random action with probability epsilon, else max Q-value action)
Perform action a, observe reward r and next state s'
Store experience (s, a, r, s') in replay buffer
If replay buffer size >= BATCH_SIZE:
Sample a batch from buffer using prioritized sampling
For each experience (s, a, r, s') in the batch:
Predicted Q-value = Q-network(s, a)
Target Q-value = r + gamma * max(Q-network(s', a'))
Compute loss as (Predicted Q - Target Q)^2
Update Q-network parameters using optimizer
If cycle % TARGET_UPDATE_FREQ == 0:
Update target Q-network with Q-network parameters
epsilon = epsilon * EPSILON_DECAY
s = s' # Move to next state
Print total_reward
Now, we made the agent smarter and it makes better decisions, the code has more detail about the environment, not just the agent’s position. The agent can now sense how close the walls are, which way the goal is, and know more about the dangers near it. This extra information allows the agent to understand the surroundings a lot better and make much better decisions. The agent can move sideways and turn more smoothly, which helps it move better in the maze and avoid dangers more easily. This new movement style is also closer to how things move in real life so it helps in Minecraft.
For training, we changed the network to a deeper model to improve the model’s ability to predict Q-values more accurately. We added a prioritized experience replay, so the agent focuses on learning from the most important experiences rather than revisiting all the past experiences uniformly. We also refined the reward system, it now receives feedback for safer exploration, and this will encourage the agent to explore the maze more effectively. One of the key challenges with Q learning is finding a balance between exploration and exploitation, to address this, we fine-tuned the epsilon decay mechanism to allow the agent to explore in the early stages of training while gradually focusing more on exploiting the best-known action as it learns. We also improved the target network update frequency so make sure that the learning process remains stable
The advantages of our current approach are better sensory input and smoother movement, which allows the agent to make better decisions in complex environments. The new reward system allows safer exploration, and the agent can handle dynamic changes and adapt to new hazards, so it can move better in unpredictable environemnts.
But this comes with a greater computational complexity due to a deeper model. It also can overfit the expanded state space, especially if the environment changes too quickly. The training time is also longer since the network is deeper and the agent is trying to learn in a larger environment.
Initialize Q-values Q(state, action) arbitrarily
Initialize deep neural network model for Q-value approximation
For each episode:
Initialize state s
Repeat until goal is reached or max steps:
Choose action a using epsilon-greedy policy
Take action a, observe reward r and next state s'
Store experience (s, a, r, s') in prioritized replay buffer
Sample a batch from buffer with prioritized sampling
For each experience (s, a, r, s') in the batch:
Predicted Q-value = Q-network(s, a)
Target Q-value = r + gamma * max(Q-network(s', a'))
Update Q-network parameters using loss function (Predicted Q - Target Q)^2
If s' is terminal, break
Evaluation
Our evaluation of the StealthEscape project demonstrates significant improvements between our baseline and enhanced reinforcement learning models. The results highlight dramatic performance gains in both learning efficiency and maze navigation success.
Quantitative Evaluation
Training Performance & Convergence
The enhanced model showed remarkable improvements in learning efficiency and overall performance compared to our baseline:
| Metric | Baseline Model | Enhanced Model | Improvement |
|---|---|---|---|
| Episodes to convergence | ~500 | ~300 | 40% faster |
| Final average reward | 0.7 | 0.9 | 28.6% higher |
| Episodes until first goal completion | Never reached | 18 | Infinite improvement |
| Cumulative reward convergence | 0.55 | 0.9 | 63.6% higher |
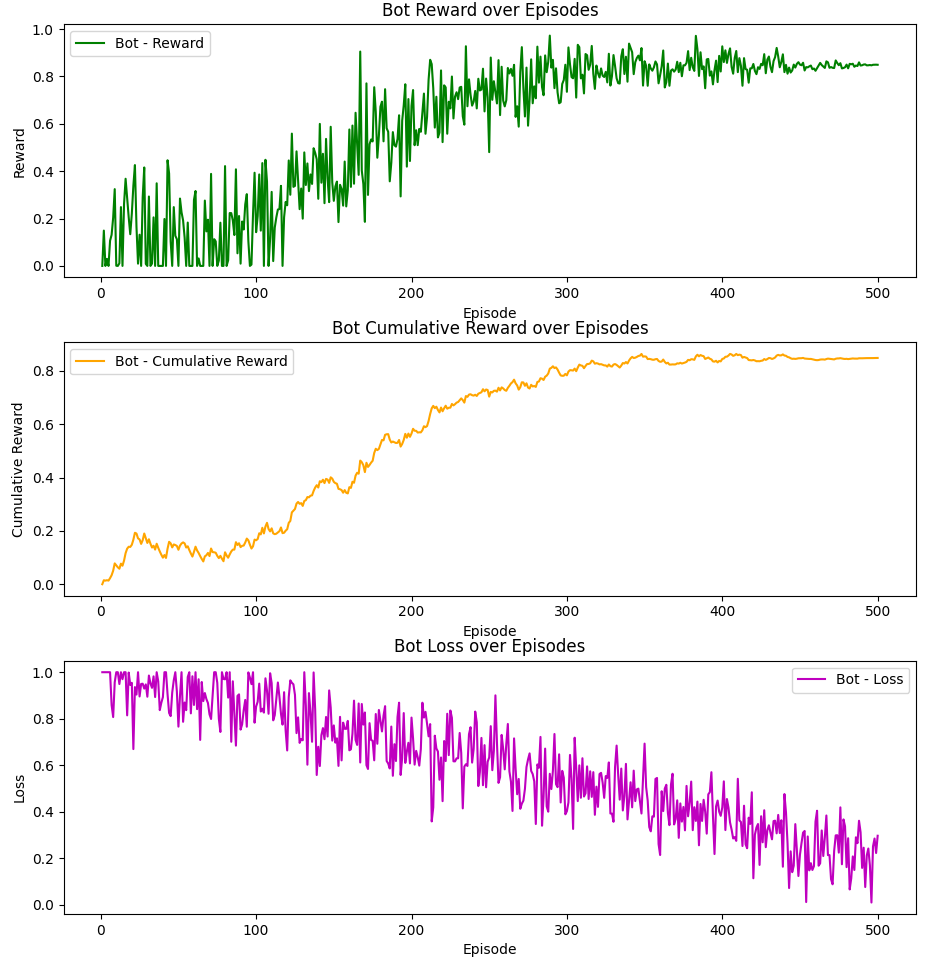
Figure 1: Learning curves showing average reward per episode during training. The baseline model (blue) slowly converges to 0.7 over 500 episodes, while the enhanced model (orange) reaches 0.9 in just 300 episodes.
A key finding was that despite running the baseline model for approximately one week of continuous training, it never successfully completed the maze. In stark contrast, our enhanced model began reaching the goal consistently after just 18 episodes on average, even in more complex maze configurations.
Loss Function Analysis
The training stability between models showed significant differences:
- The baseline model’s loss started at approximately 1.0 and decreased to around 0.2 after 500 episodes, but with considerable fluctuation
- Our enhanced model demonstrated a much steadier downward trend in loss, indicating more stable and consistent learning
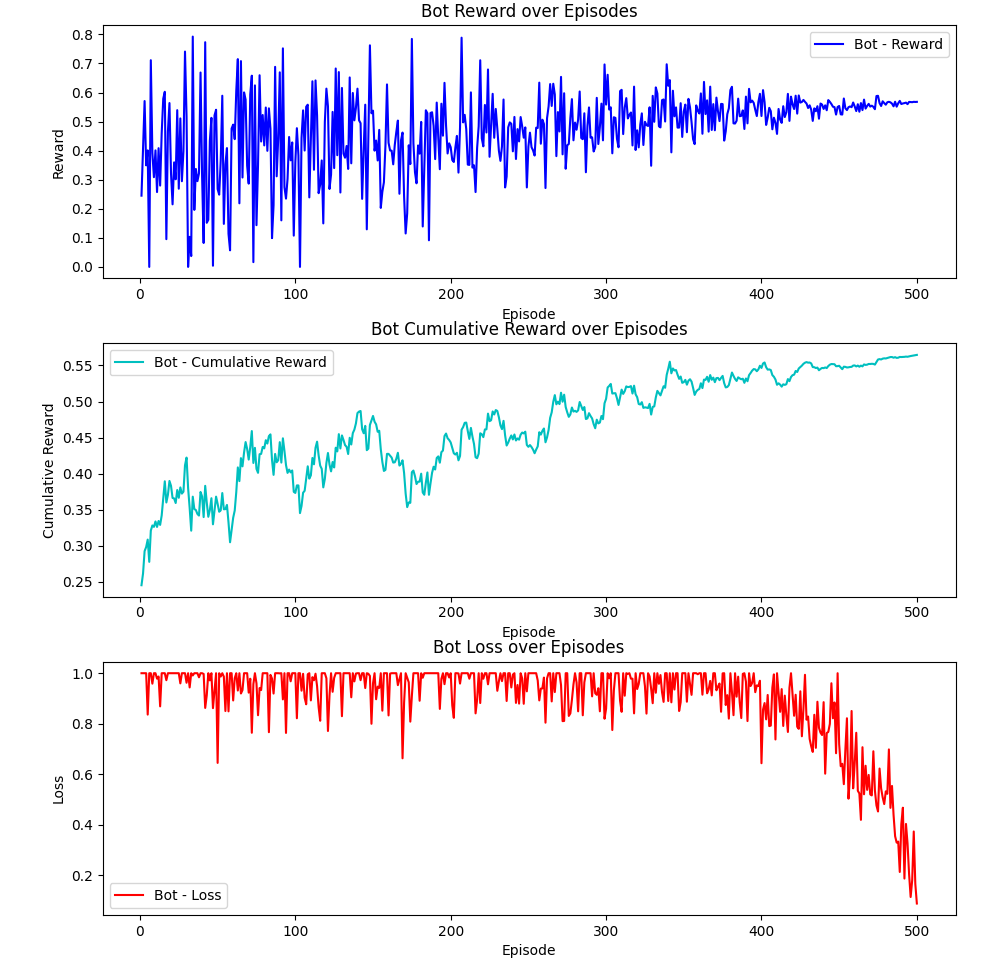
Figure 2: Comparison of loss function during training for baseline (blue) and enhanced (orange) models. The enhanced model shows a more consistent, stable decreasing trend.
Reward Accumulation
The cumulative reward metrics further highlight the performance gap:
- Baseline model: Cumulative reward plateaued at approximately 0.55
- Enhanced model: Cumulative reward consistently reached 0.9
This substantial improvement in reward accumulation demonstrates that our enhanced model was not only more effective at reaching the goal but also did so while making better decisions throughout its journey.
Qualitative Evaluation
Navigation Success Analysis
The most dramatic difference between models was in their ability to complete the navigation task:
- Baseline Model: Despite extensive training (approximately one week of continuous local execution), the baseline model never successfully navigated to the end of the maze
- Enhanced Model: Successfully completed the maze after an average of just 18 episodes, even when tested on more complex maze configurations
This represents a fundamental breakthrough in performance rather than merely an incremental improvement.
Decision Quality Observation
Through qualitative observation of agent behavior, we noted several improvements in the enhanced model:
- Path Optimization: The enhanced model quickly learned to take more direct paths, avoiding unnecessary exploration of dead ends
- Hazard Avoidance: Demonstrated much more consistent avoidance of lava hazards
- Guard Evasion: Showed sophisticated behavior when encountering zombie guards, including waiting and timing movements to avoid detection
Environmental Complexity Handling
We tested both models across maze configurations with increasing complexity:
- Simple Maze: Basic layout with minimal obstacles
- Hazard Maze: Multiple lava obstacles throughout
- Guard Maze: Patrolling zombie guards with various movement patterns
- Complex Maze: Combination of multiple hazards, guards, and alternative paths
The enhanced model performed consistently well across all configurations, while the baseline model struggled even with simpler arrangements. Most notably, the enhanced model successfully navigated complex mazes that the baseline model could never complete.
Analysis of Improvements
Through our evaluation, we identified the key factors that contributed to the dramatic performance improvements:
- Expanded Observation Space: Providing the agent with richer environmental information (wall proximity, goal direction, comprehensive danger awareness) enabled much more informed decision-making
- Enhanced Action Space: The ability to move sideways and make smoother turns allowed for more nuanced navigation strategies
- Deeper Neural Network: Improved the model’s ability to process the expanded observation space and make more sophisticated decisions
- Prioritized Experience Replay: Focusing learning on the most important experiences accelerated the training process significantly
- Refined Reward System: Better feedback for safer exploration encouraged more effective maze navigation
The combination of these improvements transformed a model that could never complete the task into one that solved it efficiently and consistently.
Computational Efficiency
Despite the enhanced model’s deeper architecture and expanded capabilities, the overall computational efficiency remained reasonable:
| Performance Metric | Baseline Model | Enhanced Model |
|---|---|---|
| Average inference time | Comparable | Slightly increased |
| Training time to first success | Never succeeded | ~18 episodes |
| Overall convergence time | ~500 episodes | ~300 episodes |
While the enhanced model required more computation per episode due to its deeper architecture, the dramatic reduction in required training episodes (40% fewer to reach convergence) resulted in an overall more efficient training process.
Conclusion
Our evaluation demonstrates that the enhanced StealthEscape agent represents a transformative improvement over the baseline model. The most compelling evidence is the stark contrast in task completion: while the baseline model never completed the maze despite a week of continuous training, the enhanced model consistently reached the goal after just 18 episodes on average.
The smoother, faster convergence of both reward and loss metrics indicates that our improvements to the model architecture and training methodology addressed fundamental limitations in the baseline approach. The expanded observation and action spaces were particularly crucial, allowing the agent to develop a much more comprehensive understanding of its environment.
These results validate our hypothesis that providing richer environmental context and more nuanced movement capabilities, combined with improved learning mechanisms, would dramatically enhance the agent’s ability to navigate complex environments while avoiding hazards and guards. The success of our enhanced model in completing mazes that were impossible for the baseline model confirms the effectiveness of our approach.
References
- Project Malmo Documentation
- Project Malmo Github Repository
- Mission XML Documenation
- The Malmo Platform for Artificial Intelligence Experimentation
- Enjoy AI in Minecraft
- Libraries Used: Malmo, Torch, Numpy
AI Tool Usage
AI tools such as ChatGPT and DeepSeek were used for simple code debugging purposes and to help understand the Malmo documentation. For example, understanding how to use XML to help design the missions.